随机过程

简介
稳定过程
随机变量的微积分
正态随机过程
记数过程
- 独立增量
- 静态增量
泊松过程

这是我在阅读这个课程讲义时做的笔记。它介绍了很多随机过程的概念。阅读它需要「概率论」的基本概念。

简介

随机过程的概念

source

股票价格 ( $S$ ) 是随机过程。想象一个 K 线图。对于任何时刻 $t_i$，我们认为「这个时刻」的价格是一个随机变量。如果我们全知全能，我们可以写出这个随机变量 $S(t_i)$ 的 PDF。

因为一个 $t$ 对应了一个随机变量 $S(t)$，那么「所有的时刻」对应了很多随机变量。我们把它们写成

\[\left\lbrace S(t), t \in [0, \infty] \right\rbrace\]

总之，

A random process is a collection of random variables usually indexed by time.

实际上，时间是连续的。我们把这样的随机变量叫做 continuous-time random process。即使是一小段时间内，理论上也有无限多的随机变量被包含在随机过程中。

如果我们把时间看成由离散的时间点组成，那么我们就有 discrete-time random process，有时也被称为 random sequences。如果我们将时间视为一天一天的，那么我们就会得到离散的时间。

观察到一个具体的随机过程，例如，看到一个具体公司股票价格的涨跌，$S(t)$。这个行为可以看成是进行了一次实验，代表样本空间（所有平行世界）里的一次采样。这样得到的，具体的 $S(t)$ 被称为 sample function 或者 sample path，它同样被称为（抽象的）$S(t)$ 的一个实现。

CDF

从现在开始我们用 $X(t)$ 来表示一个随机过程。在时刻 $t_0$，$X(t_0)$ 是一个随机变量，其 CDF 为

\[F_{X\left(t_{0}\right)}(x)=P\left(X\left(t_{0}\right) \leq x\right)\]

对这个过程中，两个时刻 $t_1$ 和 $t_2$ 的联合 CDF 为

\[F_{X\left(t_{1}\right) X\left(t_{2}\right)}\left(x_{1}, x_{2}\right)=P\left(X\left(t_{1}\right) \leq x_{1}, X\left(t_{2}\right) \leq x_{2}\right)\]

类似的我们也可以写出 PDF。

平均函数

对于随机过程 $\left\lbrace X(t),\ t \in J \right\rbrace$，其「平均函数」$\mu_{X}(t): J \rightarrow \mathbb{R}$ 为

\[\mu_{X}(t) = E[X(t)]\]

（这个定义对连续和离散随机过程都成立）

一个具体的例子是，不同月份的平均气温：

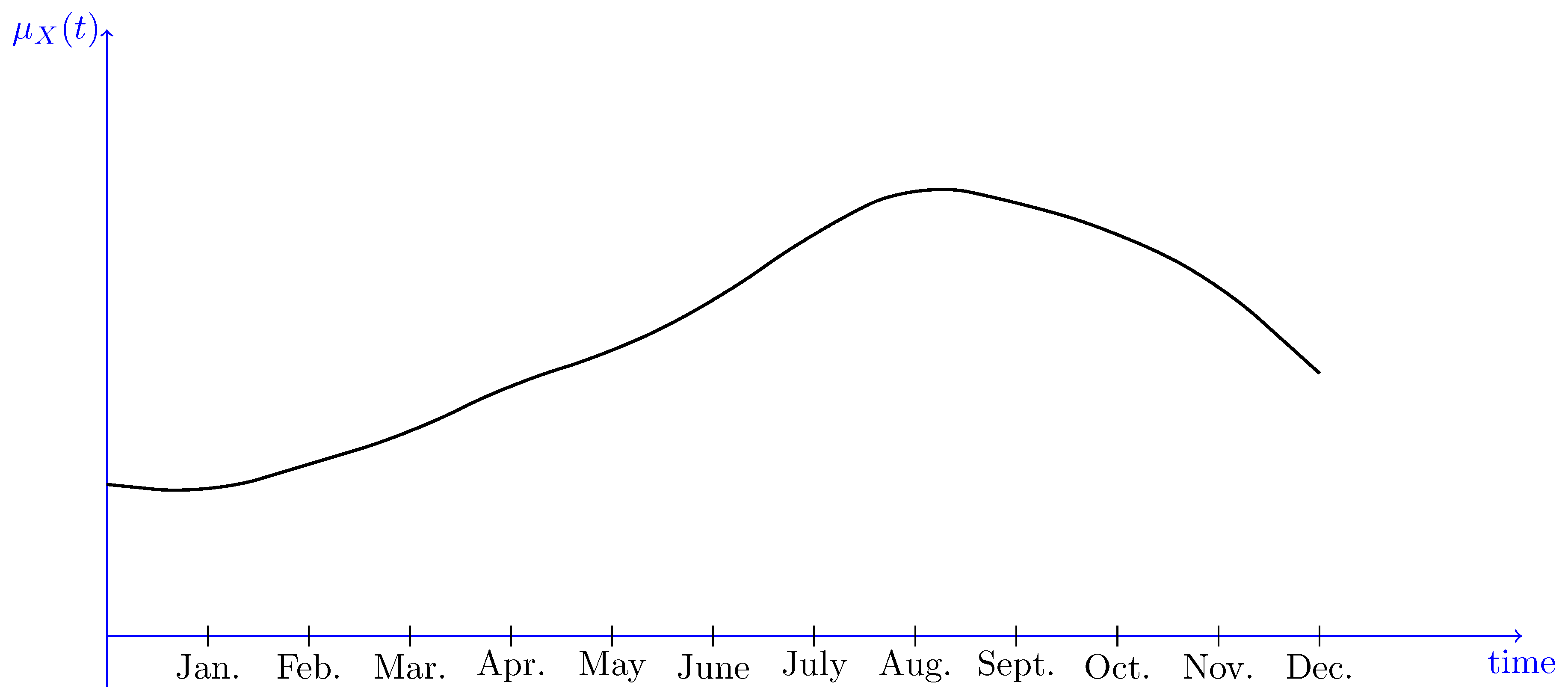
关联函数

对于随机过程 $\left\lbrace X(t),\ t \in J \right\rbrace$，它的「自关联函数」$R_X$ 以及「自协方差函数」$C_X$ 分别为

\[\begin{aligned} R_X(t_1, t_2) &= E[\ X(t_1) X(t_2)\ ] \\[1em] C_X(t_1, t_2) &= E[X(t_1)\;X(t_2)] - E[X(t_1)]\;E[X(t_2)]\\ &= R_X(t_1, t_2) - \mu_X(t_1)\mu_X(t_2) \\ &= E\left\lbrack \left( X(t_1) - E[ X(t_1)] \right) \left( X(t_2) - E[ X(t_2)]\right) \right\rbrack \end{aligned}\]

这个函数告诉我们随机过程的 两个时刻 如何关联。

多个随机过程

我们有时候想要知道，多个随机过程之间的关系。比如说，两家公司的股票价格是否相关。这个时候我们需要的，其实是多个随机过程的 cross-correlation 以及 cross-covariance。

对于两个随机变量 $\left\lbrace X(t),\ t \in J \right\rbrace$ 和 $\left\lbrace Y(t),\ t \in J \right\rbrace$

\[\begin{aligned} R_{X Y}\left(t_{1}, t_{2}\right)&=E\left[X\left(t_{1}\right) Y\left(t_{2}\right)\right] \\[1em] C_{X Y}\left(t_{1}, t_{2}\right) &=\operatorname{Cov}\left(X\left(t_{1}\right), Y\left(t_{2}\right)\right) \\ &=R_{X Y}\left(t_{1}, t_{2}\right)-\mu_{X}\left(t_{1}\right) \mu_{Y}\left(t_{2}\right) \end{aligned}\]

两个「独立随机过程」的 cross-covariance 为零。

稳定过程

当一个随机过程的统计量不随着时间改变，我们说这个过程是一个「稳定过程」。

理想情况，strict-sense stationary

理想情况下，这个不变的统计量，是所有时间，对应的随机变量的 joint CDF。

当随机过程满足下面的等式，我们称之为稳定过程，

\[F_{X\left(t_{1}\right) X\left(t_{2}\right) \cdots X\left(t_{r}\right)}\left(x_{1}, x_{2}, \cdots, x_{r}\right)=F_{X\left(t_{1}+\Delta\right) X\left(t_{2}+\Delta\right) \cdots X\left(t_{r}+\Delta\right)}\left(x_{1}, x_{2}, \cdots, x_{r}\right)\]

等式中，将时间增加 $\Delta$ 没有改变 joint CDF。

实际情况，weak-sense stationary WSS

上面的理想情况在现实中很难存在（例如，全球变暖影响了一切）。即使存在，也很难证明。有一个更弱的稳定条件。

这个条件是，对任意的 $t_1, t_2, \Delta \in \mathbb{R}$，下式成立。

\[\begin{aligned} E[X(t_1)] &= E[X(t_2)] \\ E[X(t_1 + \Delta)] &= E[X(t_2 + \Delta)] \end{aligned}\]

具体而言，对连续随机过程，有

\[\begin{aligned} \mu_X(t) &= \mu_X & \text{for all }t \in \mathbb{R}\\ R_X(t_1, t_2) &= R_X(t_2 - t_1) & \text{for all } t_1, t_2 \in \mathbb{R} \end{aligned}\]

对离散随机过程，有

\[\begin{aligned} \mu_X(n) &= \mu_X & \text{for all }n \in \mathbb{Z}\\ R_X(n_1, n_2) &= R_X(n_2 - n_1) & \text{for all } n_1, n_2 \in \mathbb{Z} \end{aligned}\]

例子：证明随机过程 WSS

定义连续随机过程 ${ X(t),\ t \in \mathbb{R}}$ 为

\[X(t) = \cos(t + U)\]

并且 $U$ 是 $[0, 2\pi]$ 上的均匀分布。证明 $X(t)$ WSS。

证明平均函数为常数

\[\begin{aligned} \mu_X(t) &= E[X(t)] \\ &= E[\cos(t + U)] \\ &= \int du\ p(u) \cos(t + u) & (\text{Uniform: } p(u)=\frac{1}{2\pi}) \\ &= \int_0^{2\pi} du \frac1{2\pi} \cos(t+u) \\ &=0 \end{aligned}\]

使用我心爱的 Mathematica

exp = 1 / 2 \[Pi] Cos[t + u];
Integrate[exp, {u, 0, 2 \[Pi]}]
-> 0

证明关联函数与时刻无关

\[\begin{aligned} R_X(t_1, t_2) &= E[X(t_1)\ X(t_2)]\\ &= E[\cos(t_1 + U)\ \cos(t_2 + U)] \\ &\left(\ \cos(a)\cos(b) = \frac12 \cos(a-b)+\cos(a+b)\ \right)\\ &= \frac12 E[\cos(t_1 - t_2) + \cos(t_1 + t_2 + 2U)] \\ &= \frac12\cos(t_1 - t_2) + \underbrace{ \frac12 \int_0^{2\pi} du \frac2{2\pi} \cos(t_1 + t_2 + 2u)}_{=0} \\ &= \frac12\cos(t_1 - t_2) \end{aligned}\]

WSS 过程的关联函数的性质

由于对 WSS 过程，$R_X(t_1, t_2) = R_X(t_1 - t_2)$ 所以重要的是时间差 $\tau = t_1 - t_2$，所以我们这样写此过程的 ACF

\[\begin{aligned} R_X(\tau) &= E[X(t) X(t - \tau)] \\ &= E[X(t + \tau) X(t)] \end{aligned}\]

考虑 ${ X(t),\ t \in \mathbb{R}}$，它的关联函数是 $R_X(\tau)$ 是

\[R_X(0) = E[X(t)^2]\]

我们将 $E[X(t)^2]$ 称为 $X(t)$ 在时刻 $t$ 的 expected (average) power。

仔细研究，我们可以得到关联函数的如下性质

\[\begin{aligned} R_X(0) &= E[X(t)^2] \ge 0 \\ R_X(\tau) &= R_X(-\tau) \\ |R_X(\tau)| &\le R_X(0) \end{aligned}\]

一些可能的 $R_X(\tau)$ 的形状是，

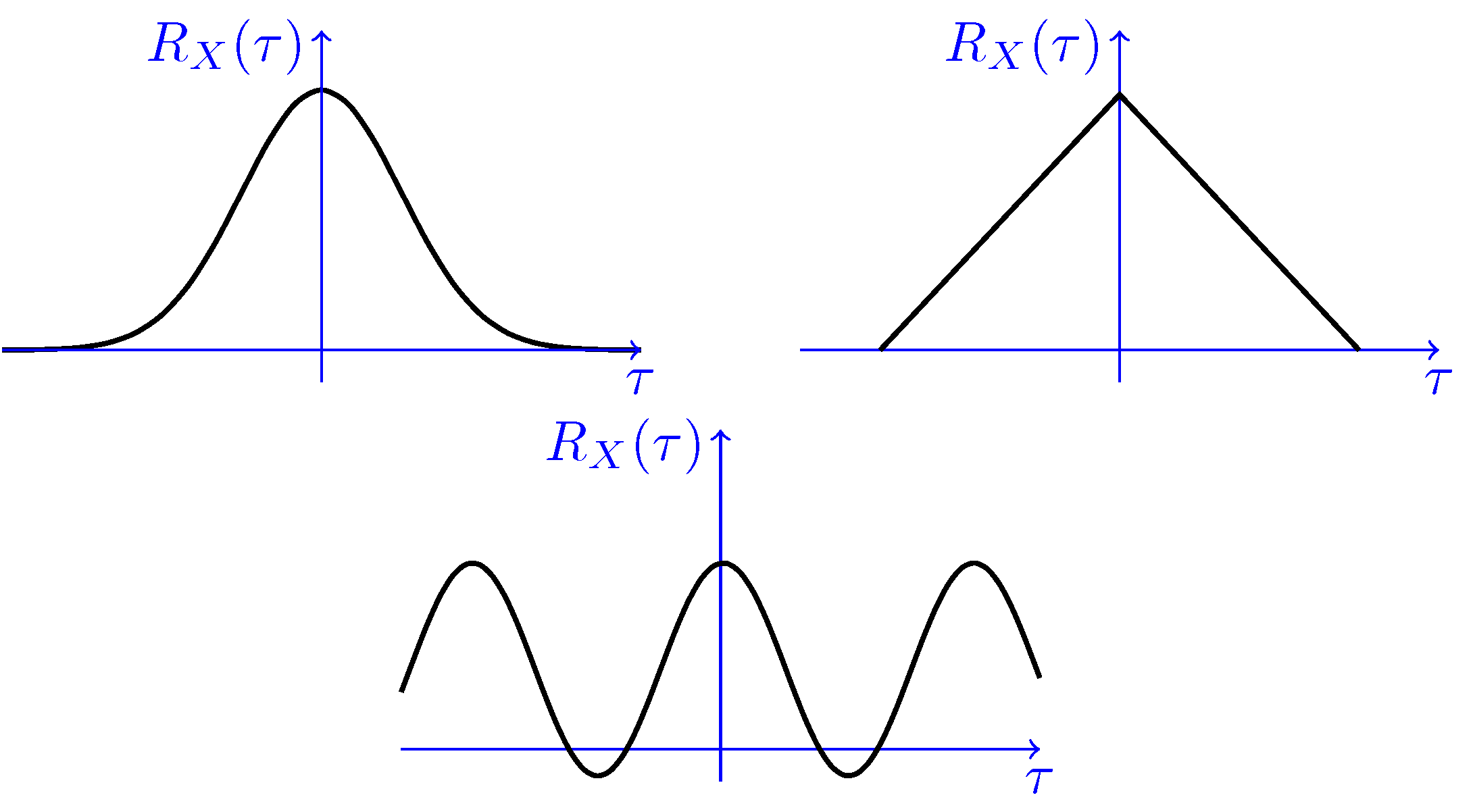
联合 WSS 过程

对于两个随机过程 $\left\{ X(t), t \in \mathbb{R} \right\}$ 和 $\left\{ Y(t), t \in \mathbb{R} \right\}$，如果它们满足下面连个条件，则称这两个过程是联合 WSS 过程，

$X(t)$ 和 $Y(t)$ 分别是 WSS 过程。
$R_{XY}(t_1, t_2) = R_{XY}(t_1 - t_2)$

循环稳定过程

严格 cyclostationary

有一些随机过程具有周期性，被称为 cyclostationary processes。更正规的描述是，随机变量

\[X(t_1),X(t_2), \cdots, X(t_r)\]

和下面的随机变量具有相同的 joint CDF。

\[X(t_1 + T),X(t_2 + T), \cdots, X(t_r + T)\]

一个严格的 cyclostationary 过程的例子是：对于随机过程 ${X(t), t \in \mathbb{R}}$，并且

\[X(t) = A \cos(\omega t)\]

其中 $A$ 是一个随机变量。很容易证明

\[\begin{aligned} X\left(t + \frac{2\pi}{\omega}\right) &= A \cos(\omega t + 2\pi) \\ &= A \cos(\omega t) = X(t) \end{aligned}\]

Weak-sense Cyclostationary, WSC

对于连续随机过程 ${X(t), t \in \mathbb{R}}$，如果存在正实数 $T$ 满足

\[\begin{aligned} \mu_X(t+T) &= \mu_X(t) & \text{for all } t \in \mathbb{R} \\ R_X(t_1 + T, t_2 + T) &= R_X(t_1, t_2) & \text{for all }t_1, t_2 \in \mathbb{R} \end{aligned}\]

随机变量的微积分

很多现实中的动力学是通过微分方程描述的。如果「随机性」混在了里面，我们需要对系统里的随机性来进行微积分。

均方连续

假设 $X(t)$ 是连续时间随机过程，我们说 $X(t)$ 在时间 $t$ 满足 mean-square continuous，如果满足下面的关系

\[\lim _{\delta \rightarrow 0} E\left[\left|X(t+\delta)-X(t)\right|^{2}\right]=0\]

这个关系的特点是，它不要求 $X(t)$ 的每一个实现都是连续函数。只要平均而言 $X(t+\delta) - X(t)$ 很小就可以了。

微积分

定义了 mean-square continuous 之后，我们可以将「可微」和「可积」的概念延伸到「均方可微」以及「均方可积」。假设 $X(t)$ 是一个随机过程，那么它的微分

\[Y(t) = \frac{d}{dt}X(t)\]

也是一个随机过程。

例子

假设我们有下面的随机过程

\[\begin{aligned} X(t) &= A + Bt + Ct^2 & t \in [0, \infty) \end{aligned}\]

其中 $A, B, C$ 均为随机变量，那么 $X(t)$ 的微分是

\[\begin{aligned} X'(t) &= B + 2 Ct & t \in [0, \infty) \end{aligned}\]

处理微积分

忽略掉具体的数学细节，处理随机过程的微积分的关键点是

differentiation and integration are linear operations

这代表着，微积分操作和求期望操作的「顺序」是可以替换的（如果 $X(t)$ 的微分 well defined）。

\[\begin{aligned} E\left[ \int_0^t X(u) du \right] &= \int_0^tE[X(u)]du \\[0.5em] E\left[ \frac{d}{dt}X(t) \right] &=\frac{d}{dt}E[X(t)] \end{aligned}\]

另一个例子

对于随机过程 $X(t)$ 和它的微分 $X’(t) = \frac{d}{dt}X(t)$，证明

\[R_{XX'}(t_1, t_2) = \frac{\partial}{\partial t_2} R_X(t_1, t_2)\]

证明过程

由 cross-correlation 的定义

\[R_{XY}(t_1, t_2) = E[X(t_1)Y(t_2)]\]

有

\[\begin{aligned} R_{XX'}(t_1, t_2) &= E[X(t_1)X'(t_2)]\\[1em] &=E\left[X(t_1)\frac{d}{d\color{tomato}{t_2}}X(\color{tomato}{t_2})\right] \\[1em] &= E\left[\frac{\partial}{\partial \color{tomato}{t_2}}X(\color{tomato}{t_2})X(t_1)\right] \\[1em] &= \frac{\partial}{\partial \color{tomato}{t_2}} E\left[X(t_1)X(\color{tomato}{t_2})\right] & \text{exchangable}\\[1em] &= \frac{\partial}{\partial t_2} R_X(t_1, t_2) \end{aligned}\]

正态随机过程

Jointly normal

如果对于很多随机变量 $X_1, X_2, \dots X_n$，对任意 $a_i \in \mathbb{R}$

\[a_1 X_1 + a_2 X_2 + \dots + a_nX_n\]

都是一个正态随机变量，则说明 $X_1, X_2, \dots X_n$ 是 jointly normal

正态随机矢量

对于随机变量构成的矢量

\[\mathbf{X} = \begin{bmatrix} X_1 \\ X_2 \\ \vdots \\X_n \end{bmatrix}\]

其中 $X_1, X_2, \dots X_n$ jointly normal，则这个矢量是正态随机变量，normal random vector。如果正态随机变量 $\mathbf{X}$ 的均值是 $\mathbf{m}$，协方差矩阵是 $\mathbf{C}$，则 $\mathbf{X}$ 的 joint PDF 是

\[f_\mathbf{X}(\mathbf{x}) = \frac{1}{(2\pi)^{\frac{n}{2}}\sqrt{\det\mathbf{C}}}\; \exp \left\{ -\frac12(\mathbf{x - m})^T \mathbf{C}^{-1}(\mathbf{x-m}) \right\}\]

正态随机过程

对于随机过程 ${ X(t), t \in J }$，如果对于所有

\[t_1, t_2, \dots, t_n \in J\]

随机变量 $X(t_1), X(t_2), \dots, X(t_n)$ jointly normal，那么这个随机过程就是「正态随机过程」(Gaussian (normal) random process)。

正态随机过程的一个特点是，如果 $X(t)$ 满足 WSS，那么 $X(t)$ 是严格的稳定过程。

联合正态过程

对于两个随机过程 ${ X(t), t \in J }$ 和 ${ Y(t), t \in J }$，如果对于任何的 $t_1, t_2, \dots, t_m$ 和 $t_1^\prime, t_2^\prime, \dots, t_m^\prime$，下面的随机变量们

\[X(t_1), X(t_2), \cdots, X(t_m),\ Y(t_1), Y(t_2), \cdots, Y(t_m)\]

jointly normal，则 $X(t)$ 与 $Y(t)$ 是联合正态过程。

如果两个联合正态过程 $X(t)$ 与 $Y(t)$ 不相关，

\[\begin{aligned} C_{XY}(t_1, t_2) &= 0 &\text{for all }t_1, t_2 \end{aligned}\]

则 $X(t)$ 和 $Y(t)$ 是两个独立的随机变量。

记数过程

对随机过程 ${ N(t), t\in[0, \infty) }$，如果 $N(t)$ 是从时刻 $0$ 到时刻 $t$ 的「事件发生次数」，则此过程被称为「记数过程」(Counting Process)。

对于记数过程，我们假设

$N(0)=0$
对于所有 $t \in [0, \infty)$ 有，$N(t) \in {0, 1, 2, \cdots}$
对于时刻 $s$， $0 \le s < t$，则 $N(t) - N(s)$ 表示时间间隔 $(s, t]$ 内，事件发生的次数。

由于记数过程最常见的例子是「顾客到达商场」，所以我们把记数过程中发生的事件叫做「到达」。

独立增量

（简而言之就是，随机过程每个时刻的「增量」都是独立的。）

对于连续时间过程 ${ X(t), t\in[0, \infty)}$，如果对于所有的 $0\le t_1 < t_2 < \cdots < t_n$，下面的随机变量们

\[X(t_2) - X(t_1),\ X(t_3) - X(t_2)，\cdots , X(t_n) - X(t_{n-1})\]

都是独立的，那么 $X(t)$ 拥有独立增量。

静态增量

对于连续时间随机变量 ${ X(t), t\in[0, \infty)}$。如果对于所有的 $t_2 > t_1 \ge 0$ 以及所有的 $r > 0$，随机变量

\[X(t_2) - X(t_1)\]

和

\[X(t_2 + r) - X(t_1 + r)\]

具有相同的概率分布。那么，我们说 $X(t)$ 具有「独立增量」。

换言之，如果随机变量的增量只依赖于时间差，不依赖于时间点，那么随机变量就拥有静态增量。

泊松过程

「泊松过程」是最常见的一种计数过程。这个过程的情形是，某种事件会随机发生，但是仿佛有一个内在的固定速率。

一个例子是，我们知道「地震」的发生是随机的。但是从历史上来看，地震发生的「速率」是 2 次 / 月。不过除了「速率」这个信息，地震的发生是彻底随机的。

泊松随机变量

令 $X$ 为一个泊松随机变量。它的参数为 $\mu$，写作 $X \sim \mathrm{Possion}(\mu)$。如果 $X$ 的取值范围是 $R_X = {0, 1, 2, \dots }$，那么，$X$ 的概率质量函数 (PMF) 是

\[P_{X}(k)=\left\{\begin{array}{ll}\frac{e^{-\mu} \mu^{k}}{k !} & \text { for } k \in R_{X} \\ 0 & \text { otherwise }\end{array}\right.\]

泊松过程具有三个值得注意的性质

$E[X] = \mu$; $\mathrm{Var}[X] = \mu$
如果一组随机变量 $X_i \sim \mathrm{Possion}(\mu_i)$，且这些随机变量都相互独立。那么 $\sum_i{X_i} \sim \mathrm{Possion}(\sum_i{\mu_i})$
泊松分布是二项分布的极限情况。（取样间隔无限短）

泊松过程的描述

假设某件事的发生是彻底随机的，不过发生的「速率」是 $\lambda$。

我们通过将「时间」分割成小段区间，来研究事件的「到达」。下面是时间分割的一个图示。

我们将第 $k$ 个间隔写作 $\left( (k-1) \delta, k \delta\right]$。在每一个「间隔」中，我们获得一个「到达」的概率为

\[\begin{aligned} P(H) &= p &(\text{binomial distribution})\\[0.5em] &= \lambda \delta &\left(\frac{\text{arrival chance}}{\text{time}} \times \text{time}\right) \end{aligned}\]

只要我们的时间间隔 $\delta$ 无限小，那么我们总可以保证每个间隔「最多只有一个到达」。一个具体的图像是

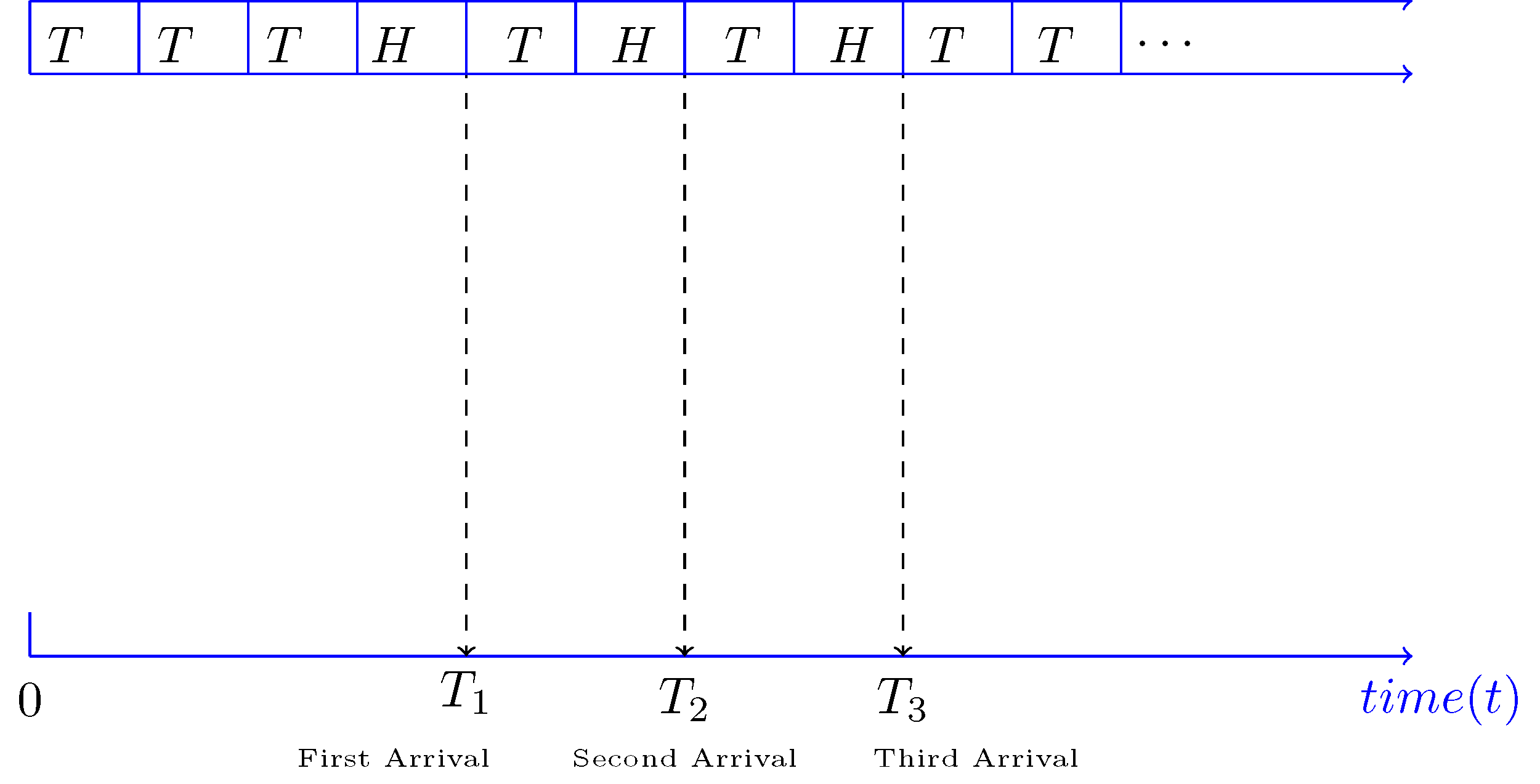
如果我们定义 $N(t)$ 为从事件 $t=0$ 到 $t=t$ 的「到达次数」，那么 $N(t) \sim \mathrm{Binomial}(n, p), \; p = \lambda \delta$。在 $\delta \rightarrow 0$ 的情况下，$N(t) \sim \mathrm{Possion}(\lambda t)$。

更进一步，我们可以发现在 任意时间间隔 $\tau$ 内，到达次数服从 $\mathrm{Possion}(\lambda \tau)$。（与初始时间无关）。

泊松过程的定义 1

在任意时间段 $\lambda > 0$ 内，计数过程 $\{ N(t), t \in [0, \infty) \}$ 如果满足下面的条件，则被定义为 泊松过程

$N(0) = 0$
随机过程 $N(t)$ 拥有「独立增量」。
任意时间段 $\tau$ 内的 到达次数 服从泊松分布 $\mathrm{Possion}(\lambda \tau)$

泊松过程的定义 2

我们可以根据「增量」来给出泊松过程的另一个定义。让我们考察连续时间里的一个小时间段 $\Delta$。如果我们研究的过程是泊松过程，那么

\[\begin{aligned} P(N(\Delta)=0) &=e^{-\lambda \Delta} \\ &=1-\lambda \Delta+\frac{\lambda^{2}}{2} \Delta^{2}-\cdots \text { (Taylor Series) } \\ &=1-\lambda \Delta+o(\Delta) \\[1em] P(N(\Delta)=1) &= \lambda \Delta + o(\Delta) \\[1em] P(N(\Delta)\ge2) &= o(\Delta) \end{aligned}\]

这个推导得到了泊松过程的第二种定义

$N(0) = 0$
随机过程 $N(t)$ 拥有「独立、静态的增量」。
下面的等式成立

\[\begin{aligned} P(N(\Delta)=0) &=1-\lambda \Delta+o(\Delta) \\[1em] P(N(\Delta)=1) &= \lambda \Delta + o(\Delta) \\[1em] P(N(\Delta)\ge2) &= o(\Delta) \end{aligned}\]

到达时间

假设 $N(t)$ 是速率为 $\lambda$ 的泊松过程。令 $X_1$ 为第一次「到达」事件发生的时间。那么 $X_1$ 是一个随机变量。我们可以根据泊松分布写出

\[\begin{aligned} P(X_1 > t) &= P(\ \text{no arrival in }(0, t]\ ) \\ &= \exp(-\lambda t) \end{aligned}\]

据此我们可以写出 $X_1$ 的 PDF

\[F_{X_{1}}(t)=\left\{\begin{array}{ll}1-e^{-\lambda t} & t>0 \\ 0 & \text { otherwise }\end{array}\right.\]

且我们发现泊松过程的到达时间服从指数分布

间隔时间

假设 $N(t)$ 是速率为 $\lambda$ 的泊松过程。令 $X_2$ 为第一次到达事件和第二次到达事件之间的「间隔」。那么 $X_2$ 也是一个随机变量。我们可以根据泊松分布写出

\[\begin{aligned} P\left(X_{2}>t \mid X_{1}=s\right) &=P\left(\text { no arrival in }(s, s+t] \mid X_{1}=s\right) \\ &=P(\text { no arrivals in }(s, s+t]) \text { (independent increments) } \\ &=e^{-\lambda t} \end{aligned}\]

我们发现 泊松过程的间隔时间也服从指数分布。

推广到任意的第 $i$ 个间隔时间，对于泊松过程，它们服从指数分布。

此外，服从指数分布的随机变量没有记忆。即，

\[P(X>x+a \mid X>a)=P(X>x), \text { for } a, x \geq 0\]

这个和泊松过程中，每个间隔相互独立是一致的。

Gamma 分布

现在让我们考虑「到达时间的分布」，它们可以写成

\[\begin{aligned} T_{1} &= X_{1} \\ T_{2}&=X_{1}+X_{2} \\ T_{3}&=X_{1}+X_{2}+X_{3} \\ &\dots \end{aligned}\]

对于第 $n$ 次到达事件，到达时间 $T_n$ 这个随机变量是 $n$ 个独立的、服从泊松分布的随机变量的和。我们把 $T_n$ 服从的分布称为 Gamma 分布，也叫 Erlang 分布。

\[\begin{aligned} T_n &= \sum_i^n{X_i} \\[1em] &\sim \mathrm{Gamma}(n, \lambda) & \mathrm{for}\ n = 1, 2, 3, \dots \end{aligned}\]

我们可以写出 Gamma 分布的 PDF：

\[\begin{aligned} f_{T_n}(t) &= \frac{\lambda^n t^{n-1}\exp(-\lambda t)}{(n-1)!} &( t > 0) \end{aligned}\]

此外，由于我们知道 $X$ 的期望和方差，

\[\begin{aligned} \mathrm{E}[X] &= \lambda^{-1} \\ \mathrm{Var}[X] &= \lambda^{-2} \end{aligned}\]

则 Gamma 分布的期望和方差是

\[\begin{aligned} \mathrm{E}[T_n] &= n \mathrm{E}[X] = n\lambda^{-1} \\ \mathrm{Var}[T_n] &= n \mathrm{Var}[X] = \lambda^{-2} \end{aligned}\]

模拟泊松过程

一个实际模拟泊松过程的方法如下。假设速率为 $\lambda$。

生成 $n$ 个 i.i.d. 的随机变量 $X_1, X_2, X_3, \dots$，其中 $X_i \sim \mathrm{Exponential}(\lambda)$
通过对 $X_i$ 求和得到每个事件的到达时间

\[\begin{aligned} T_{1} &= X_{1} \\ T_{2}&=X_{1}+X_{2} \\ T_{3}&=X_{1}+X_{2}+X_{3} \\ &\dots \end{aligned}\]